Méthode de Gauss pour échelonner une famille de vecteurs
Soit
 un espace vectoriel de dimension finie et
un espace vectoriel de dimension finie et
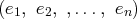 , une base de
, une base de
 .
On se donne une famille de vecteurs de
.
On se donne une famille de vecteurs de
 ,
,
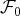 , par leurs composantes dans la base
, par leurs composantes dans la base
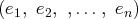 . En utilisant des opérations élémentaires, on peut transformer cette
famille
. En utilisant des opérations élémentaires, on peut transformer cette
famille
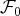 en une nouvelle famille
en une nouvelle famille
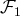 de vecteurs de
de vecteurs de
 , plus simple, avec conservation
d’un certain nombre de propriétes de la famille et en particulier :
, plus simple, avec conservation
d’un certain nombre de propriétes de la famille et en particulier :
 .
.
La transformation sur la famille se fait en suivant la même stratégie que la méthode de
Gauss pour la résolution de systèmes linéaires. Mais cette fois au lieu de faire des opérations
sur des équations, on opère sur des vecteurs.
Les opérations élémentaires ”autorisées” qui conservent les propriétés citées précédemment
sont
Échelonner la famille, c’est faire apparaître des
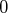 successivement sur les lignes des composantes
des vecteurs dans une base donnée.
successivement sur les lignes des composantes
des vecteurs dans une base donnée.
Plus précisément, qu’est-ce qu’une famille échelonnée ?
Comment échelonner une famille de vecteurs ?
Un échelonnement concret
Pour comprendre l’algorithme regardons comment il fonctionne sur un exemple.
Dans cet algorithme, il faut garder en mémoire les opérations effectuées.
Pour notre exemple, nous choisissons une famille de 4 vecteurs
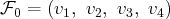 donnés par leurs composantes dans une base
donnés par leurs composantes dans une base
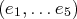 , dans un espace de
dimension 5 sur
, dans un espace de
dimension 5 sur
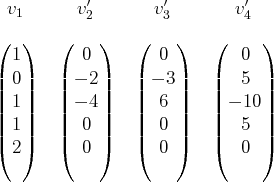
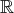 . Nous avons choisi de disposer ces données de la manière
suivante :
. Nous avons choisi de disposer ces données de la manière
suivante :
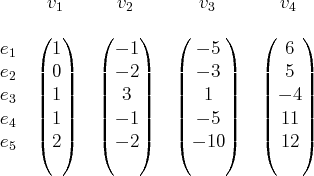
Par la suite, lorsqu’il n’y a pas d’ambiguité, nous n’écrirons pas les vecteurs de base. La
première composante de
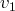 va nous servir de ”pivot” pour annuler les premières
composantes des vecteurs suivants. Ces transformations élémentaires sur les vecteurs nous
donnent la famille
va nous servir de ”pivot” pour annuler les premières
composantes des vecteurs suivants. Ces transformations élémentaires sur les vecteurs nous
donnent la famille
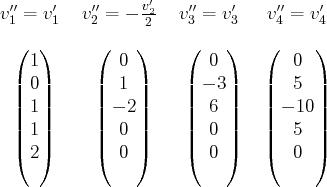
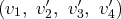 avec
avec
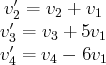
dont les composantes dans la base
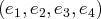 sont :
sont :
Pour faciliter la suite des calculs on divise
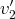 par
par
 .
.
On utilise ensuite le
 , deuxième composante non nulle de
, deuxième composante non nulle de
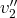 pour agir sur la deuxième
composante des vecteurs suivants.
pour agir sur la deuxième
composante des vecteurs suivants.
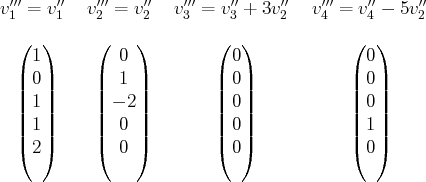
On cherche alors dans les
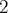 derniers vecteurs la première composante non nulle (ici la
quatrième). Comme cette composante figure dans le dernier vecteur, ce pivot ne sera pas
utilisé et l’algorithme s’arrête. Pour finir, on effectue une permutation pour placer les
vecteurs nuls en dernière position.
derniers vecteurs la première composante non nulle (ici la
quatrième). Comme cette composante figure dans le dernier vecteur, ce pivot ne sera pas
utilisé et l’algorithme s’arrête. Pour finir, on effectue une permutation pour placer les
vecteurs nuls en dernière position.
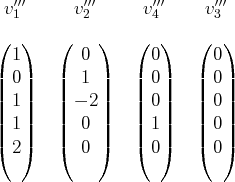
On dit que cette famille
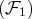 a été obtenue par échelonnement de la famille
a été obtenue par échelonnement de la famille
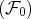 .
.
Pourquoi échelonner ? (illustré par l’exemple précédent)
Lorsque l’on a obtenu, à l’aide d’opérations élémentaires, une famille échelonnée, on
peut répondre à un certain nombre de questions sur la famille initiale. Selon la question
que l’on se pose on utilisera ou non la présence de vecteurs nuls dans la famille
échelonnée.
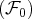 est conservé par les opérations
élementaires. De plus, on ne change pas l’espace vectoriel engendré en
éliminant les vecteurs nuls. Donc
est conservé par les opérations
élementaires. De plus, on ne change pas l’espace vectoriel engendré en
éliminant les vecteurs nuls. Donc
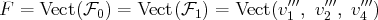
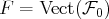 , est conservé et la famille
, est conservé et la famille
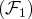 est de rang
est de rang
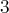 : elle ne contient que
: elle ne contient que
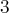 vecteurs non nuls et formant
une famille libre puisque échelonnée. Ainsi
vecteurs non nuls et formant
une famille libre puisque échelonnée. Ainsi
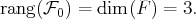
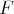 :
:
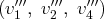 .
Cette base est plus simple pour calculer dans
.
Cette base est plus simple pour calculer dans
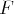 . Si l’on souhaite compléter
cette base de
. Si l’on souhaite compléter
cette base de
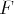 en une base de l’espace, il nous suffit de régulariser les
marches de notre escalier, en intercalant un vecteur, le plus ”simple” possible
entre
en une base de l’espace, il nous suffit de régulariser les
marches de notre escalier, en intercalant un vecteur, le plus ”simple” possible
entre
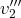 et
et
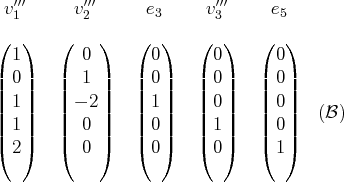
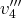 et en adjoignant un dernier vecteur. On obtient
une base
et en adjoignant un dernier vecteur. On obtient
une base
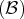 de l’espace vectoriel
de l’espace vectoriel
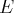 complétant la base de
complétant la base de
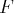 :
:
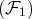 contient un vecteur nul. Donc la famille initiale est liée. Un
petit calcul permet de déduire de
contient un vecteur nul. Donc la famille initiale est liée. Un
petit calcul permet de déduire de
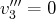 une relation linéaire non évidente
entre les vecteurs de la famille
une relation linéaire non évidente
entre les vecteurs de la famille
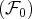 :
:
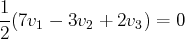
Ainsi la famille
 est liée.
est liée.
Dans le cas où la famille échelonnée ne contient aucun vecteur nul, la famille
initiale est libre.
Si l’on prend soin de garder les éventuels vecteurs nuls au cours de
l’algorithme, on peut dire que la famille initiale est libre si et seulement si la
famille déduite par échelonnement l’est.
 , on peut utiliser
la ou les relations trouvées précédemment. Ici, cette relation permet
d’éliminer un générateur. En écrivant par exemple :
, on peut utiliser
la ou les relations trouvées précédemment. Ici, cette relation permet
d’éliminer un générateur. En écrivant par exemple :
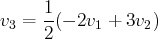
on voit que
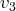 est dans
est dans
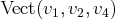 . Ainsi
. Ainsi
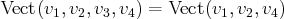 . La famille des
. La famille des
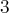 vecteurs
vecteurs
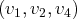 est génératrice de cet espace de
dimension
est génératrice de cet espace de
dimension
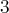 . C’est donc une base de
. C’est donc une base de
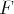 , extraite de la famille
, extraite de la famille
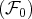 .
.
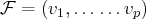 par ses composantes dans une
base donnée
par ses composantes dans une
base donnée
 :
:
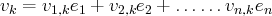 . Nous représenterons
cette famille de la manière suivante :
. Nous représenterons
cette famille de la manière suivante :
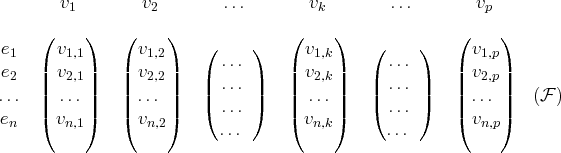
Pour les vecteurs
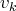 non nuls de cette famille, notons
non nuls de cette famille, notons
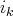 l’indice de la première
coordonnée non nulle de
l’indice de la première
coordonnée non nulle de
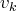 .
.
On dit que cette famille est échelonnée dans la base
 si il existe un
si il existe un
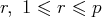 tel que pour
tel que pour
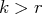 on a
on a
 (les vecteurs nuls sont les derniers de la
famille) et pour les vecteurs non nuls
(les vecteurs nuls sont les derniers de la
famille) et pour les vecteurs non nuls
 la suite
la suite
 est strictement
croissante de telle sorte que, dans la présentation précédente, les coordonnées des
vecteurs sont nulles au-dessus d’un escalier dont les marches sont de hauteur variable.
est strictement
croissante de telle sorte que, dans la présentation précédente, les coordonnées des
vecteurs sont nulles au-dessus d’un escalier dont les marches sont de hauteur variable.
Voici un exemple de famille
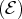 échelonnée dans
échelonnée dans
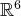 :
:
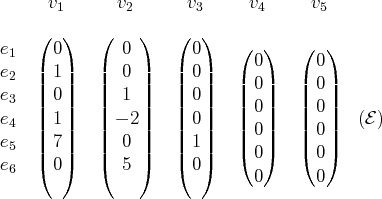
L’intérêt de travailler sur une famille échelonnée, est le résultat suivant :
Théorème : les vecteurs non nuls d’une famille échelonnée forment une famille
libre.
D’autres échelonnements possibles
Nous avons décrit une famille échelonnée avec des
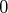 en haut à droite.
en haut à droite.
Si on intervertit l’ordre des vecteurs nous dirons encore que la famille est échelonnée
mais cette fois les
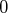 se trouvent en haut à gauche.
se trouvent en haut à gauche.
On peut aussi permuter l’ordre des vecteurs de la base et dans ce cas les
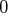 se
positionnent en bas à droite (ou à gauche si l’on a aussi permuté les
se
positionnent en bas à droite (ou à gauche si l’on a aussi permuté les
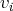 ). Les propriétés
de la famille sont, bien sûr, conservées par toutes ces permutations.
). Les propriétés
de la famille sont, bien sûr, conservées par toutes ces permutations.
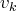 possédant une première coordonnée
possédant une première coordonnée
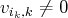 on
place ce vecteur
on
place ce vecteur
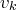 en premier et on l’utilise pour opérer sur les autres vecteurs
et annuler la
en premier et on l’utilise pour opérer sur les autres vecteurs
et annuler la
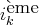 composante des autres vecteurs
composante des autres vecteurs
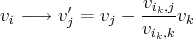 .
.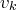 . Dans cette nouvelle famille toutes les premières coordonnées sont nulles jusqu’à la
. Dans cette nouvelle famille toutes les premières coordonnées sont nulles jusqu’à la
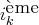 . L’algorithme s’arrête lorsqu’il ne reste plus de vecteurs ou lorsque toutes les
coordonnées des vecteurs restants sont nuls.
. L’algorithme s’arrête lorsqu’il ne reste plus de vecteurs ou lorsque toutes les
coordonnées des vecteurs restants sont nuls.Propriétés conservées par échelonnement
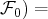 Vect(
Vect(
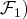
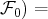 rang(
rang(
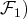
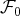 est génératrice de
est génératrice de
 si et seulement si
si et seulement si
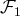 est génératrice de
est génératrice de
 .
. Propriétés conservées par échelonnement,
si l’on garde bien les vecteurs nuls au cours de l’échelonnement
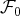 est libre si et seulement si
est libre si et seulement si
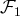 est libre, c’est-à-dire sans vecteur nul.
est libre, c’est-à-dire sans vecteur nul.
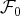 est liée si et seulement si
est liée si et seulement si
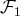 est liée. Les relations de dépendance
linéaire dans
est liée. Les relations de dépendance
linéaire dans
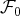 sont données par les vecteurs nuls de
sont données par les vecteurs nuls de
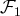 .
.